■ DH鍵交換
おね〜さんと、
ほげたんのっ!!
3 Minutes Networking、
Supplement !!
さてさて。前回、暗号化の基礎と共通鍵暗号化を説明したわよね。
「盗聴」という「脅威」からの防衛策だね。
そう。で、共通鍵暗号化方式は優れた暗号化方式で、もちろん一般的にも使用されているんだけど。
致命的な欠点があったわよね。
え〜っと、「共通鍵の受け渡し」と「鍵の数」の問題だね。
そう、「鍵の数」はまだいいとして、やはり一番の問題は「共通鍵の受け渡し」なのはわかるわよね。
そうだね、どんなに暗号化してあっても鍵自体を盗聴されて入手されたらイミないもんね。
そうよね。というわけで、公開鍵暗号化方式の登場なわけ。
なんだっけ、非対称鍵暗号化方式とも呼ばれてるんだっけ。
うんうん。で、公開鍵暗号化方式の前に、間違えられやすいものの話を先にしておこうと思って。
それは、DH鍵交換法というものなのよ。▼ link
でぃふぃーへるまん鍵交換法? 鍵を共有するの?
そう。ディフィーさんとヘルマンさんが考え出した、共通鍵を秘密裏に交換する方法。
だから、「鍵交換法」ね。IPsecなどで使われてるの。
へ〜。共通鍵暗号化方式の弱点である「鍵の受け渡し」を秘密で実行できるってことでいいのかな?
そうね、その理解でいいわ。
でね、DH鍵交換法も、公開鍵暗号化方式も、「法」の世界の話なのよ。
なんの世界?
「法」。つまり、mod、剰余を使った計算をするの。
とりあえず、x = y mod p の形でここから先は書くからね。
え〜っと、y / p = ? であまりが x って意味だったよね、その式。
で、法って何?
さっきの x = y mod p だと、pが法ね。
でで、DH鍵交換法と公開鍵暗号化方式を説明していくけど、詳しくやると数式で死ねるから、簡単にいくわね。
なんかなぁ。
いえね、これがね。数式の塊なのよ。数論、整数論ってのが元になってるからね。
ともかくともかく、DH鍵交換法、いってみよー。
[FigureSP16-01:DH鍵交換法]
え? えぇぇ?
え〜〜〜〜っと、理解できないポイントが2つ。1つ、このKってホントに一致するの?
するわよ。
- (a mod p) * b mod p = (a * b) mod p
- K = Yb ^ Xa mod p = (g ^ Xb mod p) ^ Xa mod p = (g ^ Xb) ^ Xa mod p = g ^(Xa×Xb) mod p
- K = Ya ^ Xb mod p = (g ^ Xa mod p) ^ Xb mod p = (g ^ Xa) ^ Xb mod p = g ^(Xa×Xb) mod p
ほらね。数値入れたほうがわかりやすいかな?
- p = 7 、g = 5 、Xa = 2 、Xb = 3
- Ya と Yb
- Ya = g ^ Xa mod p = 5 ^ 2 mod 7 = 25 mod 7 = 4
- Yb = g ^ Xb mod p = 5 ^ 3 mod 7 = 125 mod 7 = 6
- Kの計算
- K = Yb ^ Xa mod p = 6 ^ 2 mod 7 = 36 mod 7 = 1
- K = Ya ^ Xb mod p = 4 ^ 3 mod 7 = 64 mod 7 = 1
…ほんとだ。
ちなみにgだけど、これは任意の数値っていってるけど、一応ルールがあって、原始元って言われる値じゃなきゃダメなのね。
なんか難しいね。
で、もう1つのポイントだけど、これって最初の数値、p、gと計算結果Ya、Ybって盗聴可能だよね。Kってこの4つの数値から計算できちゃわない?
できちゃわない。それはね、離散対数問題ってのがあるから。
なにそれ?
簡単に言うと、Y = g ^ X mod p。pが十分に大きな素数の場合、gとpがわかってる状態で、XがあればYは簡単に求まるけど、YからXを求めるのは難しいってこと。直接YからXを求める方法がないのね。
へ〜〜〜。っていうことは、YaやYbがわかっても、Xa、Xbが求まらないから安全だってことかな?
ま、そういうことね。Xa、XbがないとKが求まらないからね。
ともかく、これがDH鍵交換法ね。
なんでこの話をしたんだっけ?
それは次から話す公開鍵暗号化方式と間違える人がたまにいるからよ。
DH鍵交換法は、公開情報を使うけど、目的は共通鍵を安全に交換するものってこと。暗号化じゃないよ、ってことかな。
まさしく「鍵交換」なんだね。
■ 公開鍵暗号化-RSA
さてさて〜。次は本命の公開鍵暗号化方式。
特にRSA公開鍵暗号化方式について話すわね。
その言い方だと、公開鍵暗号化方式って他にもあるように聞こえるけど?
あるわよ。例えば、さっきの離散対数問題を利用した「楕円曲線暗号」とかあるわね。
へー。
んでも、公開鍵暗号化方式といったら、「RSA」って感じなわけなのよ。
ともかくね、さっきのDH鍵交換が先にあって。「公開情報」を使ってのやりとりという発想が前提にあるわけね。
あぁ、DH鍵交換の方が、公開鍵暗号化方式より先なんだね。
そうそう。で、そこからRSAの3人が作り出したのがRSA公開鍵暗号化ってわけなのよ。
ではでは。公開鍵暗号化方式の基本からいってみよー。
[FigureSP16-02:RSA公開鍵暗号化方式]
ペアの2つの鍵、秘密鍵と公開鍵があって。
相手に公開鍵で暗号化してもらって、自分の秘密鍵で復号する。
そう。公開鍵で暗号化したものは、公開鍵では復号できないってのがポイントね。なので、公開鍵は「公開」してもかまわない。
公開鍵が盗聴されたとしても、公開鍵で暗号化されたデータを復号できない、つまり中身を盗み見る事ができないからだね。
そゆことそゆこと。
で、RSAの特徴は逆もOKってところよね。つまり、秘密鍵で暗号化したものは公開鍵で復号できるってところ。
[FigureSP16-03:RSA公開鍵暗号化方式・2]
面白いよね、これ。
でもさ、公開鍵で復号できちゃったら意味がないよね。だって公開鍵って「公開」されちゃってるから。
そうね。暗号化して「秘密裏に相手に渡す」ってことはできないわね。
でもこれはこれで大事な使い道があるからいいのよ。
そうなの?
うん。それはまた後で話すとして。
この公開鍵暗号化は思ったより簡単に数式で説明できるのよ、これが。
うぇー、また数式?
ん〜、まぁ、数式で説明しなくてもいいんだけど、公開鍵の安全性ってのは数式を理解してるとわかりやすいから。
さてさて。というわけで数式ごー。
[FigureSP16-04:RSA暗号化方式・3]
ははぁ、なんか簡単な計算に見えるんだけど…。
ん〜計算自体は簡単よね。乗算してmodするだけだから。
このRSAの計算式をもう1回まとめると。
- 大きな素数p、q
- N = p × q
- N' = (p - 1) × (q - 1)
- 1 = e × d mod N'
でもって暗号化/復号がこれ。
- E = P ^ d mod N → P = E ^ e mod N
- E = P ^ e mod N → P = E ^ d mod N
なんか、さっきのDH鍵交換でも思ったけど、ホントにこれで暗号化/復号できるの?
やってみましょっか。あまり大きな数だと大変だから、小さい数でいくわね。
- 大きな素数 2 、5
- N = p × q = 10
- N' = (p - 1) × (q - 1) = 4
- 1 = e × d mod N'
- e = 3
- d = 3
ありゃ? eとdが同じ数になっちゃってるよ。
まぁ、小さい素数でやってるからね。大きな素数でやればそんなことは起きないから。
さて、これで暗号化できるのはN以下の数値だから、0〜9の範囲ね。それぞれ暗号化してみると。
| P | P2mod10 | P3mod10 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 7 |
| 4 | 6 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 9 | 3 |
| 8 | 4 | 2 |
| 9 | 1 | 9 |
[TableSP16-01:公開鍵による暗号化]
P3mod10の列が暗号文Eになるんだね。
そう。ほげたん気づいた? P3mod10の列は0〜9の数字が全部でてるってことに。
え? あ、ホントだ。並びは違うけど、0〜9が全部ある。すごい!!
面白いわよね。例えば「3521」という数字が平文だとすると、暗号文は「7581」になるわけね。で、復号の方はこうなるわけ。
| E | E2mod10 | E3mod10 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 8 | 4 | 2 |
| 7 | 9 | 3 |
| 4 | 6 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 3 | 9 | 7 |
| 2 | 4 | 8 |
| 9 | 1 | 9 |
[TableSP16-02:秘密鍵による復号]
…すごい、ホントに戻ってる…。
さっきの例の「7581」もちゃんと「3521」だよ、おね〜さん。
でしょ。これで秘密鍵で暗号化、公開鍵で復号ってのがわかるでしょ。
公開鍵で暗号化、秘密鍵で復号も、できるのがわかるわよね。この場合両方とも3だから。
うん。でもおね〜さん、これ大丈夫なの?
公開鍵であるe = 3、N = 10があれば、dなんか簡単に求まりそうだけど。
んふふ。そうでもないのよ、これが。じゃあ考えてみましょう。dを求めるにはどうするの?
1 = e × d mod N' を計算すればいいんだよ。
そうね。でも、これはN'がないと絶対求まらないわよ。modの計算は法がないと無理だからね。
ん、ん〜〜〜。じゃあN'を求めるよ。Nがあるから、N = p × q で、pとqを求めて、N' = (p - 1) × (q - 1)を…。
はいは〜い、ほげたんストップ。「N = p × q で、pとqを求めて」と簡単に言うけど。これって「Nを素因数分解する」ってことよね。
「そいんすうぶんかい」なんて久々に聞いたけど。確かにそだね。
大きな数の素因数分解はできないのよ、ほげたん。
え? そうなの?
今だとどのくらいだろ? 500ビット(2500)の素因数分解はできるって話はきいたけど。ちなみにRSAで使われるのは512ビット、1024ビット、2048ビットなどね。
うわ、512ビットはいけそうだけど、1024とかはるか遠いよ。
でしょ。RSAはこの「大きな数の素因数分解は困難である」ってところから安全であるってなってるわけ。
ははぁ、なるほどですよ。
■ 公開鍵暗号の特徴
さてさて。この公開鍵暗号の特徴だけど。簡単にいえば、共通鍵と反対の特徴を持ってるの。まず、最大の特徴が公開鍵、この存在ね。
「公開されても秘密情報を知ることができない」鍵、でしょ。
そゆこと。つまり、共通鍵暗号化方式の鍵の受け渡し問題が発生しないわけね。
うん、確かに。共通鍵暗号化方式だとどうしても「鍵をどうやって安全に渡すか」が問題だからね。
さらに、公開鍵を1つあれば複数との暗号化/復号が可能ってところも、共通鍵とは反対よね。
そうなるのかな?
共通鍵で複数と暗号化/復号をする場合、Aさんとの暗号化のための鍵を、Bさんにも使うわけにはいかない、って理由でしょ。それだとAさんとの通信の内容がBさんにダダ漏れになっちゃうから。
うん。あ、そうか。公開鍵方式なら、暗号化して送ってもらう時は自分の公開鍵で暗号化して送ってもらうから、復号できるのは秘密鍵を持っている自分だけ。
そう、その公開鍵は1つだけでいいでしょ? つまり、不特定多数との暗号化通信に向いているってことなのよ。
そだね。共通鍵だと不特定多数と暗号化通信するのは「鍵の受け渡し」「鍵の数」どっちとっても大変だもんね。
そして、公開鍵の利点のもう1つ、PKIの骨子ともいえるのが、暗号化/復号に使う鍵の役割の入れ替えができるってところ。
暗号化鍵が秘密鍵なら、復号鍵は公開鍵。暗号化鍵が公開鍵なら、復号鍵は秘密鍵。暗号化/復号どちらか一方しか使えないってわけじゃないってことだね。すごいね、公開鍵暗号化。
そうね。だけど、公開鍵暗号化には結構な弱点が存在するのよ。
共通鍵の3DESは168ビット鍵長、AESは128ビット鍵長。でもRSAは512、1024、2048ビット鍵長。これが意味するのは?
公開鍵暗号化の方が鍵長が長い?
そう。つまり、前も話したけれど「鍵長は長い方が処理時間が長い」だったわよね。だから、暗号化/復号処理のスピードが遅いってこと。これはどういう意味だっけ?
えっと、「処理速度が速い暗号化は大きなサイズのデータを暗号化するのに適してる」だったから、「大きいサイズのデータの暗号化には適していない」ってことかな?
そういうこと。ちょっと試してみましょうか。暗号化ソフトでメジャーな、opensslのスピードテストコマンドを使うわね。 まず、比較対象として、AES128ビット鍵長CBCモードとRC4だとこう。▼ link
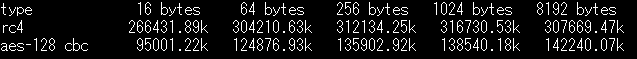
[FigureSP16-05:共通鍵暗号化方式の処理速度]
ん? どうやって見るの?
「1秒間に暗号化したビット数」ね。上の「16 bytes」とかは処理するデータのサイズ。
へぇ、データサイズが違うと処理スピードにも差がでるんだね。あぁ、そうか。ブロックのサイズで区切りが変わるからかな? RC4だと16ビット以外あまり差がないし。
たぶんね。で、256バイトのところを例にしましょうか。RC4だと、312Mビット/秒。秒で39Mバイトぐらい。AES128ビット鍵長CBCモードだと、135Mビット/秒で、秒で17Mバイトぐらいかな。
RC4はやっ!! さすがストリーム暗号。AESと倍以上違う。
うん、さすがよね。で、一方、RSA1024ビット鍵長だと。ちょっと表示が違うけどこんな感じ。

[FigureSP16-06:公開鍵暗号化方式の処理速度]
「sign」が秘密鍵を使った場合の速度、「verify」が公開鍵を使った場合ね。右の「sign/s」と「verify/s」が1秒間の処理ビット数。
秘密鍵使った場合と、公開鍵使う場合で処理速度違うの?
そうね。公開鍵暗号化では公開鍵を使う処理の方が多いので、さっきの数式思い出してほしいんだけど、1 = e × d mod N' で公開鍵のeはなるべく小さい数にするのが一般的なの。
へぇ………、おね〜さん、これ単位ビット? メガでもキロでもなく?
そうよ。
遅っ!! なにこれ、早い方の公開鍵でも11Kビット/秒? バイトだと1Kバイト強じゃん!!
パパさんのパソコン、Core2Duoなのにっ!!
そうなるわねぇ。
いやいや、おね〜さん? 共通鍵暗号だと、単位はメガだよ?
例えば、公開鍵で1Mバイトのファイルを暗号化すると、1000秒、約17分ね。
AES128ビット鍵長CBCモードだと、7ミリ秒…。17分って…。
わかったでしょ。「公開鍵暗号化は処理速度が遅い」ってことね。
遅すぎだよっ!! こんなんじゃ、遅すぎて暗号化に使えないよ。
ま、そうよね。なので、公開鍵暗号化では普通にファイルの暗号化とかはしないのよ。
じゃ、何に使うの?
例だしましょ。
[FigureSP16-07:公開鍵暗号化と共通鍵暗号化による暗号化]
なるほど、鍵の受け渡しを公開鍵で、暗号化自体は共通鍵で行うんだね。
そう、鍵ならサイズが小さい、大きくても256ビットとかだから、公開鍵暗号化でもそれほど時間はかからない。実際のデータは高速な共通鍵に任せるってことね。SSL/TLSやS/MIMEがこの方式を使ってるわ。
なるほどなるほど。
さって、公開鍵暗号化の説明その1はこのぐらいかな。公開鍵暗号化の仕組みと、暗号化をどのように行うってことを理解したかな?
「宛先の公開鍵を使って暗号化」「受信した宛先は自身の秘密鍵で復号」だね。
んで、「説明その1」ってことは「その2」もあるってこと?
逆の「送信元は自身の秘密鍵で暗号化」「受信した宛先は送信元の公開鍵で復号」の説明してないでしょ。
あー、確かに。それって、「誰でも入手できる公開鍵で復号できる」から、盗聴の防止、通信の秘匿にはならないよね。何のためにそんなのがあるのかなぁ。
それが次回の話。じゃ、まった次回。
おね〜さんと、
ほげたんのっ!!
3分間ネットワーク、
サプリメントでした〜〜〜っ!!
- DH鍵交換
-
[Diffie-Hellman Key Exchange]
DH鍵共有[Key Agreement]とも呼ぶ。参考リンクはIPAにあるRFC2631。
- 原始元
-
原始元gをべき乗すると、1からp-1までのすべての数値が求まる値gのこと。
乗数と計算結果の1からp-1までのすべての数値が対応する。
- RSA公開鍵暗号化方式
-
発明者のRivest、Shamir、Adelmanの頭文字からつけられた公開鍵暗号化方式。
公開鍵暗号化方式の中でももっとも標準として使われている。
- openssl
- オープンソースのSSL/TLSキット。今回利用したのはWindows版。公式サイトは参考リンクからどうぞ。
- 「1秒間に暗号化したビット数」
-
もちろん処理するCPUによって値は変わります。ベンチマークテストとかでもこのopensslのテストコマンドは使われていたりします。
ちなみに今回実行したCPUは、Intel Core2Duo 2.66GHz(E6750)。
 ほげたんの今日のポイント
ほげたんの今日のポイント-
- DH鍵交換法を使うと秘密裏に共通の情報を持つことができる。
- 公開鍵暗号化は「公開鍵」と「秘密鍵」を使う。
- 公開鍵で暗号化したものは秘密鍵で復号できる。
- 秘密鍵で暗号化したものは公開鍵で復号できる。
- 公開鍵暗号化は鍵を公開できるため、受け渡しや数の問題がない。
- 処理が非常に低速なため、サイズの大きいデータを暗号化するのは現実的ではない。
- 参考リンク
-
- Diffie-Hellman 鍵共有法http://www.ipa.go.jp/security/rfc/RFC2631JA.html▲
- OpenSSLhttp://www.openssl.org/▲
- OpenSSL日本語サイトhttp://www.infoscience.co.jp/technical/openssl/▲

